By: Aiyaan Hasan, International Center for AI and Cyber Security Research and Innovations (CCRI), Asia University, Taiwan, rayhasan114@gmail.com
Abstract:
As technology develops, a new area of study known as Quantum Machine Learning (QML) has developed from the combination of quantum computing with machine learning. The potential for quantum machine learning algorithms to transform pattern recognition problems is examined in this paper. These algorithms demonstrate potential in outperforming traditional methods by utilising the unique characteristics of quantum computing. The article aims to clarify the transformational intersection of quantum computing and machine learning through an investigation of quantum concepts, algorithms, practical applications, and obstacles.
Introduction:
The limits of classical computing are becoming more and more obvious in the continuously changing world of technology, especially when it comes to performing intricate pattern recognition jobs.[1] The solution offered by quantum computing is exciting because it may exist in numerous states concurrently (superposition) and retain interconnection between qubits (entanglement).[2] This article investigates the mutually beneficial link between quantum computing and machine learning, with particular emphasis on the potential for quantum machine learning algorithms to revolutionise pattern recognition.
Principles of Quantum Machine Learning:
Understanding the fundamentals of quantum physics is necessary in order to fully appreciate the potential of quantum machine learning algorithms.[3] Superposition is a property of quantum bits (qubits), which enables them to represent many states at once. The fundamentals of quantum physics are explained in this part, which lays the foundation for comprehending how qubits vary from classical bits in how they process information.
Algorithms for Quantum Pattern Recognition:
Due to its potential uses in pattern recognition, quantum algorithms like Grover’s and Shor’s algorithms have drawn interest. For example, Shor’s technique performs exceptionally well in integer factorization, a crucial cryptography problem.[4] Conversely, Grover’s approach makes it possible to quickly search across unsorted datasets, which has a direct impact on pattern matching.[5]
Grover’s Algorithm:
Introduced by Lov Grover in 1996, Grover’s algorithm is a benchmark for unstructured search problems in quantum computing.[6] The time complexity of conventional methods for searching an unsorted database is O(N), where N is the total number of objects. However, Grover’s quantum technique offers a quadratic speedup by reducing this complexity to about O(√N).
How Grover’s Algorithm Works: Grover’s algorithm’s amplitude amplification method is what gives it its strength. Grover’s approach uses quantum superposition and interference to increase the probability amplitude of the right answer, which makes it possible to find the required item more quickly in an unsorted dataset.
Use in Pattern Matching: The field of pattern recognition directly benefits from this capacity to search unstructured information quickly in pattern matching.[7] Grover’s approach provides a quantum advantage in these kinds of jobs by lowering the computing effort needed to identify a specific image in a large database or to recognize a sequence within a batch of unsorted data.
Shor’s Algorithm for Integer Factorization:
Another quantum algorithm that has attracted interest is Shor’s Algorithm for Integer Factorization, which was developed by Peter Shor in 1994.[8] It is especially well-known for its ability to solve integer factorization issues. For big numbers, classical factorization techniques are inefficient due to their exponential time complexity. Conversely, Shor’s method displays polynomial time complexity when executed on a quantum computer.
How Shor’s method Operates: Shor’s method, at its foundation, effectively factors huge integers into their prime components by utilizing the quantum Fourier transform and modular arithmetic. Thanks to its intrinsic quantum parallelism, Shor’s method explores many options at once and is much faster than classical factorization techniques.
Application in Pattern Recognition: Shor’s algorithm is useful in pattern recognition as well as cryptography, where it is mainly recognized for its ability to break some traditional encryption techniques based on the complexity of integer factorization. An essential issue in computer science is integer factorization, and Shor’s algorithm’s effective answer has relevance for activities where pattern recognition or data analysis require factorizing integers.

Quantum Machine Learning in Practise:
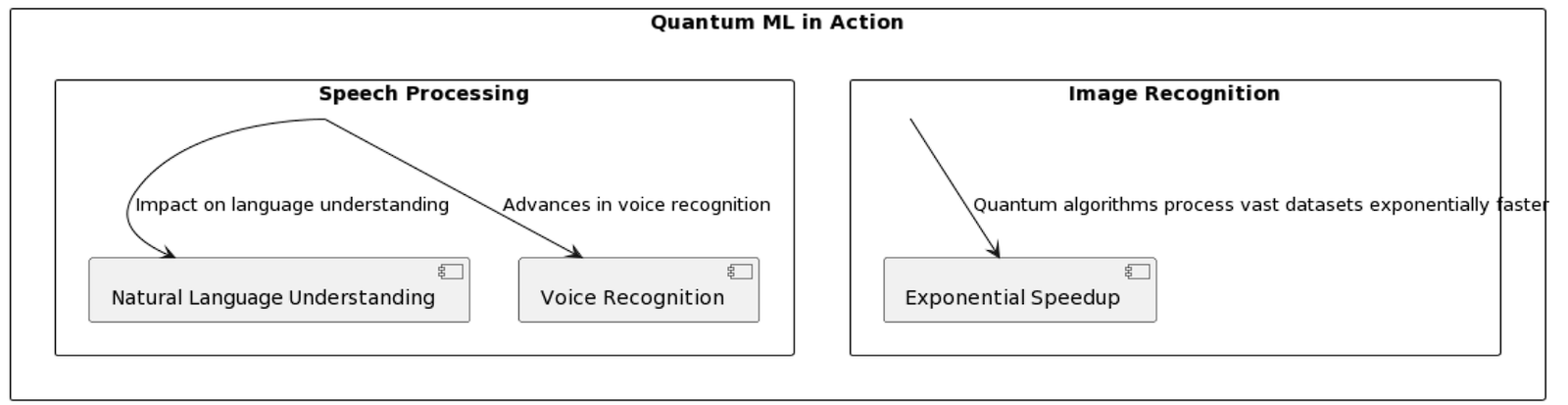
This section looks into practical applications of quantum machine learning algorithms for pattern recognition problems, going beyond theoretical concerns. Quantum algorithms have proven to analyse large datasets quicker than their conventional equivalents in the image recognition domain. Quantum algorithms have also proven beneficial for speech processing applications, demonstrating their potential influence on voice recognition and natural language understanding technology. The practical benefits of using quantum computing in machine learning for pattern recognition are demonstrated by these instances.
Issues to Take into Account:
Quantum Machine Learning Algorithms have a lot of potential applications, but there are drawbacks to their implementation. A major barrier is quantum decoherence, which is the susceptibility of qubits to outside forces. Another complex difficulty is addressing faults in quantum calculations using error correcting techniques. Furthermore, for practical and widespread use, quantum hardware has to improve beyond its current level. This section offers a thoughtful analysis of these difficulties, highlighting the significance of continued research to get over these obstacles.
Conclusion:
To sum up, quantum machine learning algorithms have a great deal of potential to transform pattern recognition. Opening up new possibilities is the combination of the special powers of quantum computing with the constantly developing field of machine learning. Pattern recognition tasks might be significantly impacted by the development of quantum technology and the exploration of the challenges associated with error correction by researchers. In order to fully realise the potential of quantum machine learning algorithms, further research and development are needed. This will pave the way for a time in the future when the combination of machine learning and quantum computing would completely transform technology.
References:
- Badertscher, C., Cojocaru, A., Colisson, L., Kashefi, E., Leichtle, D., Mantri, A., & Wallden, P. (2020, December). Security limitations of classical-client delegated quantum computing. In International Conference on the Theory and Application of Cryptology and Information Security (pp. 667-696). Cham: Springer International Publishing.
- Li, T., & Yin, Z. Q. (2016). Quantum superposition, entanglement, and state teleportation of a microorganism on an electromechanical oscillator. Science Bulletin, 61(2), 163-171.
- Biamonte, J., Wittek, P., Pancotti, N., Rebentrost, P., Wiebe, N., & Lloyd, S. (2017). Quantum machine learning. Nature, 549(7671), 195-202.
- Borders, W. A., Pervaiz, A. Z., Fukami, S., Camsari, K. Y., Ohno, H., & Datta, S. (2019). Integer factorization using stochastic magnetic tunnel junctions. Nature, 573(7774), 390-393.
- Jozsa, R. (1999). Searching in Grover’s algorithm. arXiv preprint quant-ph/9901021.
- Grassl, M., Langenberg, B., Roetteler, M., & Steinwandt, R. (2016, February). Applying Grover’s algorithm to AES: quantum resource estimates. In International Workshop on Post-Quantum Cryptography (pp. 29-43). Cham: Springer International Publishing.
- Singh, M. P., Radhey, K., & Rajput, B. S. (2018). Pattern Classifications Using Grover’s and Ventura’s Algorithms in a Two-qubits System. International Journal of Theoretical Physics, 57, 692-705.
- Ugwuishiwu, C. H., Orji, U. E., Ugwu, C. I., & Asogwa, C. N. (2020). An overview of quantum cryptography and shor’s algorithm. Int. J. Adv. Trends Comput. Sci. Eng, 9(5).
- Wang, H., Li, Z., Li, Y., Gupta, B. B., & Choi, C. (2020). Visual saliency guided complex image retrieval. Pattern Recognition Letters, 130, 64-72.
- Al-Qerem, A., Alauthman, M., Almomani, A., & Gupta, B. B. (2020). IoT transaction processing through cooperative concurrency control on fog–cloud computing environment. Soft Computing, 24, 5695-5711.
- Gupta, B. B., & Quamara, M. (2020). An overview of Internet of Things (IoT): Architectural aspects, challenges, and protocols. Concurrency and Computation: Practice and Experience, 32(21), e4946.
Cite As
Hasan A. (2023) Quantum Machine Learning Algorithms for Enhanced Pattern Recognition, Insights2Techinfo, pp.1